Door: Ruud van Oosterhout
Eindige Elementen Methode (EEM), voor betonplaten
Betonnen vloeren en wanden worden door constructeurs steeds vaker berekend met behulp van de eindige-elementenmethode (EEM). Dit artikel is geschreven om een duidelijk beeld te geven over de rekenmethodiek, en om aan te geven welke voor- en nadelen het heeft ten opzichte van ‘traditionele’ rekenmethodieken.
Rekenmethoden voor (beton)platen.
Voorafgaand aan de uitleg over EEM, worden eerst een aantal andere rekenmethodieken toegelicht.
Betonnen elementen zoals vloeren en wanden worden doorgaans geschematiseerd als 1-D lijnelementen met een breedte van 1,00 m1 en een variabele dikte. Vervolgens worden hier belastingen aan toegevoegd waaruit een momenten- en dwarskrachtenlijn volgt. Het betonnen element wordt op basis hiervan afgewapend met buigtrekwapening en indien nodig dwarskrachtwapening. Ook dient de doorbuiging en scheurvorming te worden gecontroleerd. Deze veelgebruikte methodiek wordt ook wel de strokenmethode genoemd, en wordt nog door de meeste vloerleveranciers gebruikt.
Ook kan de constructeur gebruik maken van GTB-tabellen. Deze tabellen geven momentencoëfficiënten voor wapeningsmomenten op basis van diverse randvoorwaarden. Omdat er veel voorwaarden worden gesteld aan het gebruik van de tabellen worden ze niet vaak toegepast. Er mag bijvoorbeeld alleen een gelijkmatig verdeelde belasting aanwezig zijn, er worden eisen gesteld aan de lengte- en breedteverhouding van het vloerveld en er wordt geen rekening gehouden met eventuele sparingen. Aangezien de werkelijkheid in de meeste gevallen afwijkt van de zeer vereenvoudigde schematisering van de GTB-tabellen is deze methodiek meestal niet bruikbaar.
Om deze complexere vloervelden en belastinggevallen in een 2-D EEM rekenmodel in te kunnen voeren, zijn er diverse softwarepakketten ontwikkeld. Onderstaand wordt een voorbeeld geïllustreerd met behulp van het EEM-pakket van MatrixFrame.
Rekenvoorbeeld EEM
In figuur 1 is een isometrische weergave te zien van de betonvloer die als voorbeeld wordt gebruikt. Allereerst wordt de geometrie ingevoerd, waarbij stramienen als hulpmiddel kunnen worden gebruikt. Het is mogelijk om in het XY-vlak willekeurige vloervelden te ontwerpen met diverse diktes en sparingen. In dit voorbeeld wordt een betonvloer uitgewerkt, maar het is ook mogelijk om andere materialen toe te kennen aan de plaat.
Met het definiëren van opleggingen heeft de constructeur veel vrijheid. Er kan namelijk worden gekozen voor lijn- en puntvormige ondersteuningen, die overal in het model kunnen worden geplaatst. De opleggingen in Z-richting kunnen als verende ondersteuning worden ingevoerd, en het is ook mogelijk om een (gedeeltelijke) inklemming om de X- en Y-as in te voeren. Het is zelfs mogelijk om voor verschillende gebieden een oppervlakteondersteuning te definiëren (bijvoorbeeld een grondbedding). Als de plaatgeometrie en ondersteuningen zijn ingevoerd, kunnen de belastingen worden toegevoegd.
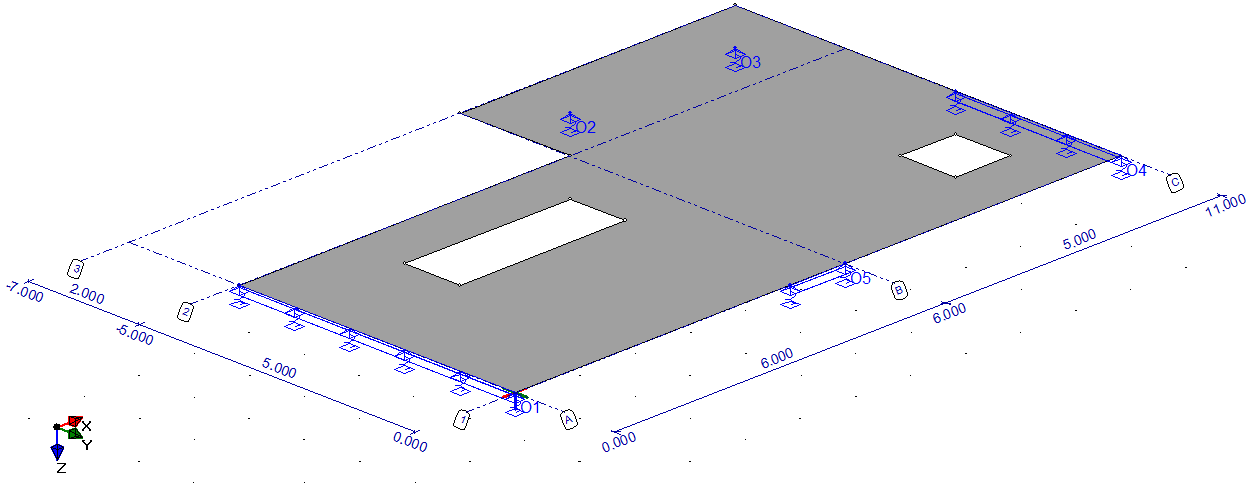
Figuur 1 Plaatgeometrie met opleggingen
Figuur 2 geeft een overzicht van de aanwezige belastingen weer. Het is mogelijk om gebieden te definiëren waarop oppervlaktebelastingen kunnen worden aangebracht [kN/m2]. Bij veranderlijke belasting is het zelfs mogelijk om velden te laten genereren ten behoeve van de belastingschikking. Er kunnen op willekeurige posities lijn- en puntlasten worden ingevoerd [kN/m1 en kN]. De meeste belasting zal in Z-richting werken, maar het is ook mogelijk om momenten om de X- en Y-as in te voeren. Belastingcombinaties met bijbehorende partiële factoren kunnen automatisch door het programma worden gegenereerd.
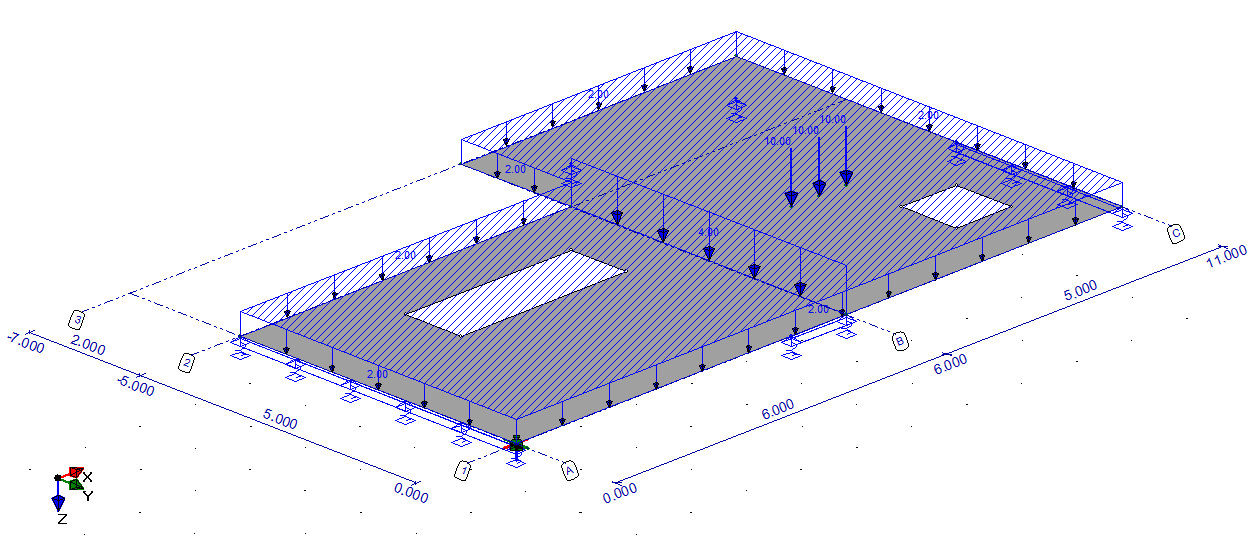
Figuur 2 Belastingen
Voordat de berekening wordt uitgevoerd wordt er een ‘mesh’ gegenereerd. Dit is een patroon van simpele elementen die aan elkaar verbonden zijn middels knooppunten (zie figuur 3). In principe wordt een complexe vorm vervangen door een samenstelling van vele eenvoudigere elementen. De accuraatheid van de berekening hangt af van het aantal elementen dat gekozen wordt. Meer elementen leidt tot een exacter resultaat maar dit vergt aanzienlijk meer rekenkracht. Als de mesh met de gewenste dichtheidsfactor is gemaakt wordt de lineair elastische berekening uitgevoerd.
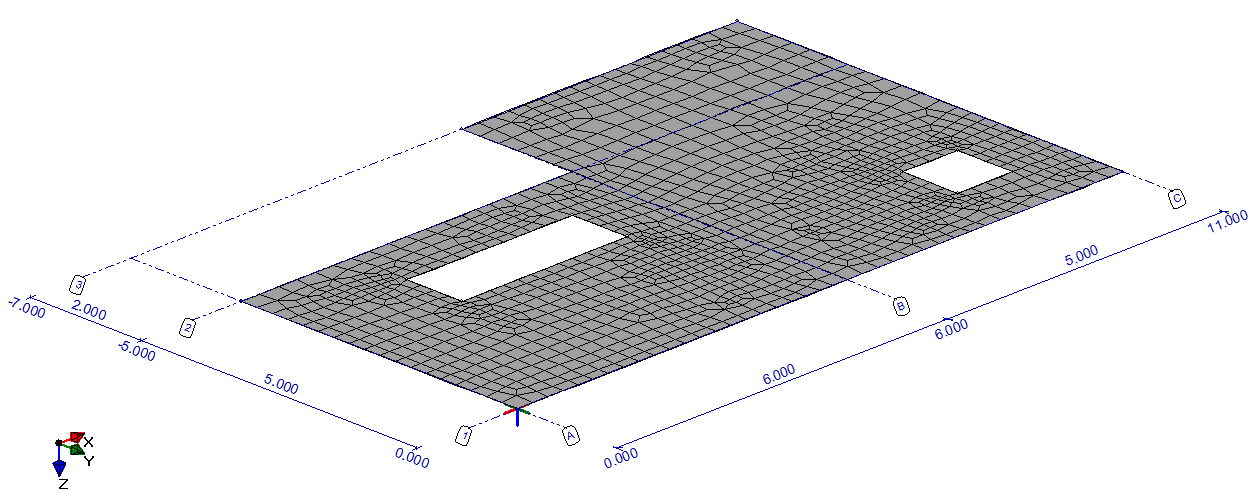
Figuur 3 Meshpatroon van het vloerveld
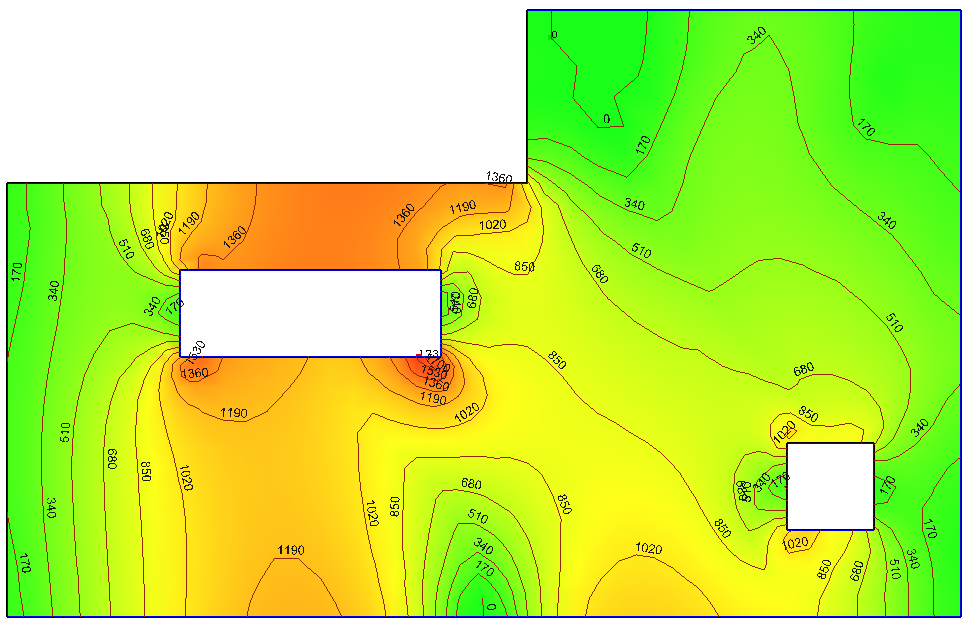
De resultaten van een EEM-berekening worden meestal weergegeven middels kleuren en isolijnen. Figuur 4 toont bijvoorbeeld de momenten in X-richting, waarbij in rood de positieve momenten en in blauw de negatieve momenten worden aangegeven. Het is ook mogelijk om vergelijkbare schema’s voor dwarskrachten en verplaatsingen weer te geven. Bij betonnen vloeren kan ervoor gekozen worden om een fictieve elasticiteitsmodule aan te nemen om de verplaatsing te kunnen benaderen, maar het is ook mogelijk om na de definitie van wapening een herberekening te doen en de (nagenoeg) exacte verplaatsingen te berekenen.
De reactiekrachten van de opleggingen kunnen, net als alle overige resultaten, per belastingcombinatie/-geval worden weergegeven. Zoals te zien in figuur 5 worden voor de puntvormige ondersteuningen reactiekrachten in kN weergegeven, en voor lijnvormige ondersteuningen in kN/m1 met een lineair verloop. Als er sprake is van een oppervlakteondersteuning worden de reacties uiteraard in kN/m2 weergegeven (bijvoorbeeld grondspanningen). Op basis hiervan kunnen eventueel onderliggende constructies zoals metselwerk, kolommen of stalen liggers worden gecontroleerd.
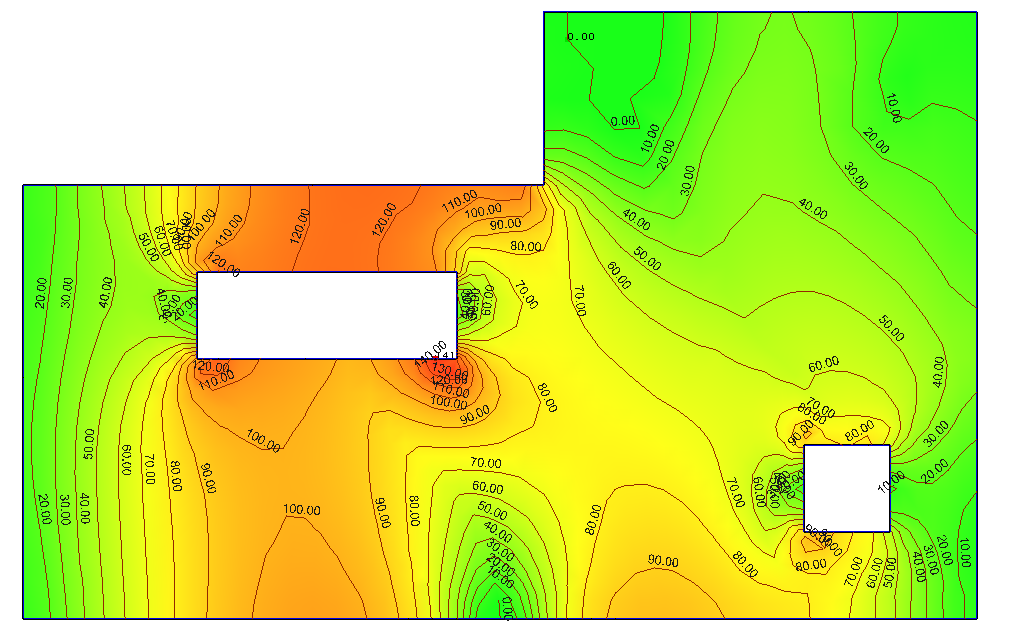

Figuur 4 Momenten in X-richting (positief en negatief)
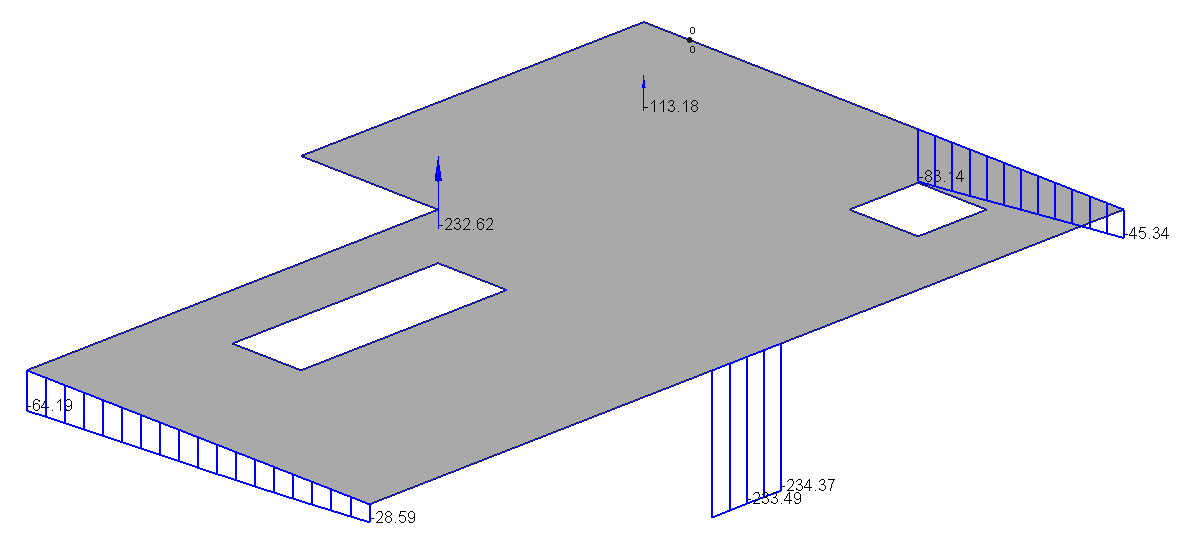
Figuur 5 Oplegreacties
Net als de momenten wordt de benodigde wapeningshoeveelheid weergegeven in kleuren met isolijnen. Hieronder (figuur 6) is bijvoorbeeld de benodigde onderwapeningshoeveelheid in X-richting zichtbaar. Uiteraard is het ook mogelijk om dit voor de bovenwapening en de Y-richting te doen. Voor overschrijdingen van de dwarskrachtcapaciteit worden waarschuwingen gegeven. Omdat de betonkwaliteit en dekking eerder is ingevoerd, kan direct de wapeningshoeveelheid op basis van de nuttige hoogte worden berekend. Het is mogelijk om voor verschillende gebieden wapeningshoeveelheden in te voeren. Als er bijvoorbeeld wordt gekozen voor een kruisnet onder en boven van Ø10-150 (520mm2/m1) in het gehele vloeroppervlak, zal alleen de resterende benodigde hoeveelheid nog zichtbaar zijn. Hier kan dan plaatselijk extra wapening worden toegevoegd, totdat alles voldoende is voorzien. Tot slot kan er nog een herberekening worden gedaan om de doorbuigingen te controleren.
Figuur 6 Benodigde wapeningshoeveelheid [mm2/m] in X-richting onder
Samenvattend
De rekenmethodiek brengt veel voordelen met zich mee: complexe vormen zijn exact te berekenen en complexe belastinggevallen kunnen eenvoudig worden gedefinieerd. Resultaten zijn vaak gunstiger dan die van de strokenmethode en worden overzichtelijk en visueel weergegeven. De invoer van alle parameters kan wel veel tijd kosten. Men moet er wel rekening mee houden dat ondeskundig gebruik kan leiden tot onrealistisch resultaat, met alle gevolgen van dien. Constructieve software blijft een hulpmiddel, een constructeur moet de resultaten niet direct als waarheid aannemen, en deze altijd kritisch blijven beoordelen.
Mocht u nog vragen hebben over deze rekenmethodiek, dan kunt u contact opnemen via r.v.oosterhout@bolwerkweekers.nl.